【Excelで計算】非定常熱伝導数値解析について解説！

はじめに
フーリエの法則
フーリエの法則の拡張
非定常熱伝導の数値解析
表計算ソフトによる解析の例
さいごに

はじめに

以前の記事では、熱交換器の伝熱計算を取り上げました。
この伝熱計算で得られる結果は定常状態の数値ですが、実用設計上は機械の立ち上げ、立ち下げ時のような非定常状態の挙動を知りたい場面もあると思います。

この記事を読むことで、単純化した1次元の非定常熱伝導計算が理解でき、表計算ソフトで数値的に解析することができるようになります。

フーリエの法則

計算を始める前に、前提となる基本法則（フーリエの法則）について解説します。
①定常状態、②材質が均一かつ一定の固体において、③1次元の熱伝導温度場を考えるとき、
伝熱量[W]は温度勾配と熱が流れる方向に直角な断面積に比例します。
比例定数は熱伝導率と呼ばれます。

\(dQ = -λ\dfrac{dT}{dx}dA\) \( \rm{[W]}\)

平たく言えば、
①固体内部の温度差が大きいときや、面積が大きいときに伝熱量が大きくなる
②同じ温度差、面積であれば、熱伝導率の大きい材料の方が伝熱量が大きくなる
ことを意味しています。
この式を積分すると、以前の記事で取り上げたニュートンの冷却法則と同じ形になります。

フーリエの法則の拡張

先ほどのフーリエの法則は定常状態で仮定していました。これを非定常状態に拡張しましょう。
下の図のような1次元温度場を考えます。物体内に熱放射や発熱、吸熱はなく、圧力も物性値も変わらないとします。
紙面には書いていませんが、検査体積の奥行、高さともに単位長さ（長さ1）であるとします。

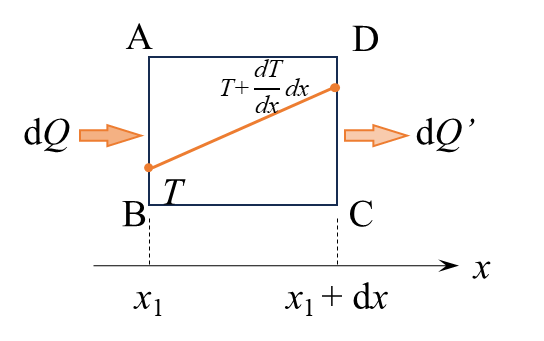
熱伝導によって時間dtの間にABからx軸方向に流れる熱量dQ[J]は、ABにおける温度がTであること、面積が1であることに注意すれば、フーリエの法則を用いて下記のようにあらわせます。
（フーリエの法則では単位がWであったが、今回は時間をかけているのでJとなっている点に注意）

\(dQ = -λ\dfrac{dT}{dx}・1・dt\)

次に、時間dtの間にCDを通る熱量dQ'[J]は、CDにおける温度がT+dT/dx*dxなので、

\(dQ’ = -λ\dfrac{d}{dx}(T+\dfrac{dT}{dx}dx)・1・dt\)

とあらわせます。（3次元の一般式と形をそろえるためにあえてdxを消去していません）

これらの式の差をとると、時間dtの間に検査体積の内部に蓄えられた熱量dQ”が計算できます。

\(dQ’’ = dQ-dQ’=λ\dfrac{d^2T}{dx^2}dxdt\)

この熱量dQ”によって、時間dtの間に検査体積内の温度は\(\dfrac{dT}{dt}dt\)、つまりdTだけ上昇したはずです。
物体の密度をρ、定圧比熱をcpとすれば、温度をdTだけ上昇させるために必要な熱量は、体積がdxであることに注意すれば

\(dQ’’ = ρc_p(\dfrac{dT}{dt}dt)dx\)

とあらわせます。よって、2つの式をつなぐと、

\(λ\dfrac{d^2T}{dx^2}dxdt=ρc_p(\dfrac{dT}{dt}dt)dx\)

⇔\(\dfrac{λ}{ρc_p}\dfrac{d^2T}{dx^2}=\dfrac{dT}{dt}\)

のように整理できて、\(a=\dfrac{λ}{ρc_p}\)とおくと、

\(\dfrac{dT}{dt}=a\dfrac{d^2T}{dx^2}\)

となります。この式をフーリエの微分方程式と呼びます。
ここで、aは熱拡散率とよばれ、非定常熱伝導における温度分布の時間変化速度の大きさに対応します。
（余談ですが、燃焼の世界では熱拡散率と物質拡散率の比をとったルイス数と呼ばれる無次元数がよく使われます。ルイス数が1より大きいときは、物質が拡散するよりも先に熱が拡散するため、燃焼に必要なエネルギーが散逸して火炎が弱まります。）

非定常熱伝導の数値解析

フーリエの微分方程式は、そのまま解こうとすると一般には解析的に複雑となることから、実用上はコンピュータを用いた数値解析が採用されることが多いです。
ここでは、導出した1次元の微分方程式を、Excelのような表計算ソフトで解析する方法を紹介します。
先ほど導出した式を差分法で離散化すると、下記のようにあらわせます。

\(\dfrac{T_{i,j+1}-T_{i,j}}{Δt}=a\dfrac{T_{i+1,j}-2T_{i,j}+T_{i-1,j}}{Δx^2}\)

⇔\(T_{i,j+1}=T_{i,j}+\dfrac{aΔt}{Δx^2}(T_{i+1,j}-2T_{i,j}+T_{i-1,j})\)

\(x=iΔx\) (i = 0, 1, 2,・・・)
\(t=jΔt\) (j = 0, 1, 2,・・・)

この式は、下記の図の状態をあらわしています。
つまり、
①時刻 j 秒における、地点 i – 1 の温度
②時刻 j 秒における、地点 i の温度
③時刻 j 秒における、地点 i + 1 の温度
がわかれば、地点 i における、時刻 j + 1 秒の温度を計算することができます。

なお、時間刻みΔtの値は、

\(Δt≦\dfrac{Δx^2}{2a}\)

を満足するように設定する必要があります。（これより粗いと発散してしまいます。このような条件をCFL条件（Courant-Friedrichs-Lewy Condition）と呼びます。）

表計算ソフトによる解析の例

解析の例として、参考文献に記載の例題を解いてみます。
直径10mm、長さ300mmの金属丸棒が、100℃で均一な温度に断熱保持されているとき、この丸棒の片端を急激に20℃に冷却し続けた場合の温度分布の時間変化を考えます。ただし、熱拡散率は30×10^-6 [m²/s]とします。

最初に空間刻みを考えます。丸棒を10等分すると、Δx=30 [mm] = 30×10^-3 [m]となります。
CFL条件から、時間刻みΔtは15s以下にする必要があるので、今回はΔt=10 [s] とします。
これより、1次元のフーリエの微分方程式は下記の通り計算できます。

\(T_{i,j+1}=T_{i,j}+0.333(T_{i+1,j}-2T_{i,j}+T_{i-1,j})\)

問題の設定から境界条件はそれぞれ100℃、20℃と、初期条件は100℃とそれぞれ設定できるので、表計算ソフト上では下記の通り計算できます。

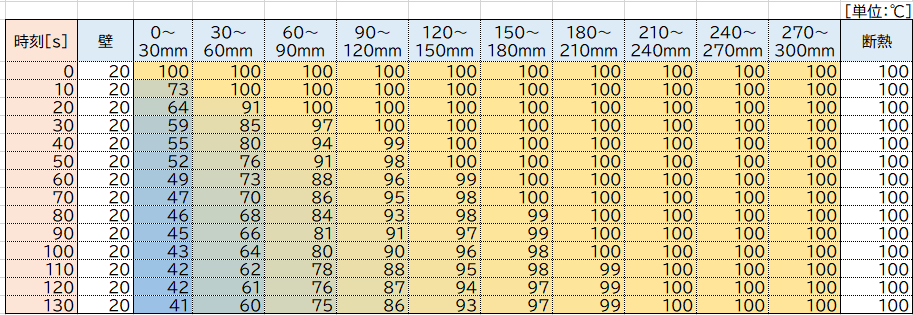
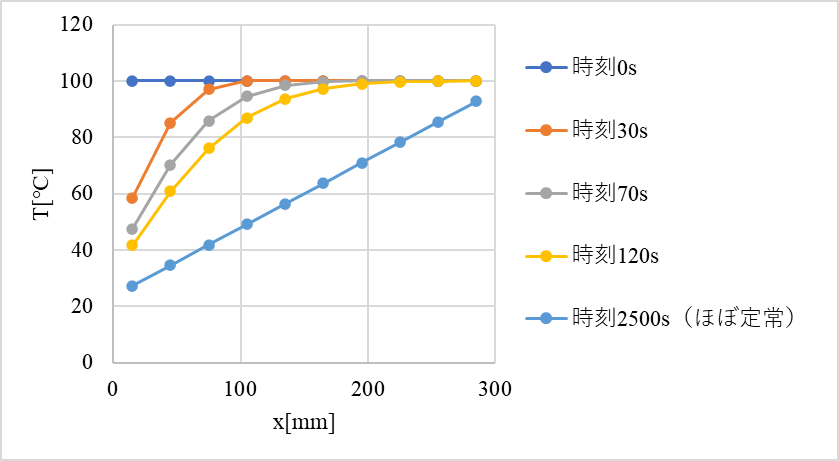
ちなみに、これらを抜粋してグラフにすると下図のようになります。
はじめは、時間の経過に従って壁側の温度がどんどん低下していきます。その時々のグラフは、指数関数形状となります。
そして、値の変化がほとんどなくなるまで時間を進めてみると、温度分布は線形となります。
これは最初に説明したフーリエの法則そのものです。