はじめに
流速と音速の比率であるマッハ数がおおむね0.3以上になると、流体の圧縮性を考慮して流れを検討する必要があります。
圧縮性流れでは、マッハ数1の状態になることをチョーク(あるいは閉塞)といいます。
このチョーク流れは、便利な点が主に2つあります。
1つ目は、チョーク部の断面積やタンク圧力、温度、気体の種類から質量流量を簡単に計算できることです。
\( m = \dfrac{P_0A}{\sqrt{RT_0}}\sqrt{γ(\dfrac{2}{γ+1})^{\frac{γ+1}{γ-1}}} \)
2つ目は、背圧の影響を受けず安定して流体を流すことができることです。
今回の記事では、このチョーク流れについて解説します。
管の断面積と流速の関係
あるゴムホースに水が流れているとします。このホースの出口を指でつまんで断面積を小さくすると、水の勢いが強くなります。
これは質量流量の式でも確認することができます。
質量流量mと密度ρが一定ならば、断面積Aが小さくなると流速uが大きくなるためです。
\( m = ρAu \)
では、断面積を絞ってどんどん加速していくとどうなるのでしょうか?
断面積Aと流速uの関係について、圧縮性を考慮した式を見てみましょう。
この式は、理想気体・等エントロピー(可逆断熱)流れを仮定したうえで、質量保存式と運動量保存式を連立することで導出できます。詳しくは参考文献を読んでみてください。
\( (1-M^2) \dfrac{du}{u} + \dfrac{dA}{A} = 0 \)
この式から、マッハ数Mによって性質が大きく変わることがわかります。
亜音速流れ(0 < M < 1)
断面積が小さくなる(dA < 0)と、速度は増加(du > 0)します。
これは、先ほどのゴムホースのイメージ通りであり、我々の感覚通りです。
超音速流れ(1 < M )
断面積が小さくなる(dA < 0)と、速度も減少(du > 0)します。
先ほどまでの感覚とは逆の傾向です。
つまり、超音速流れでは、速度を増すためには断面積を広げる必要があります。
音速流れ(M = 1)
断面積の変化率が0、すなわち断面積が極大値か極小値をとるとき、流れが音速になることを意味しています。
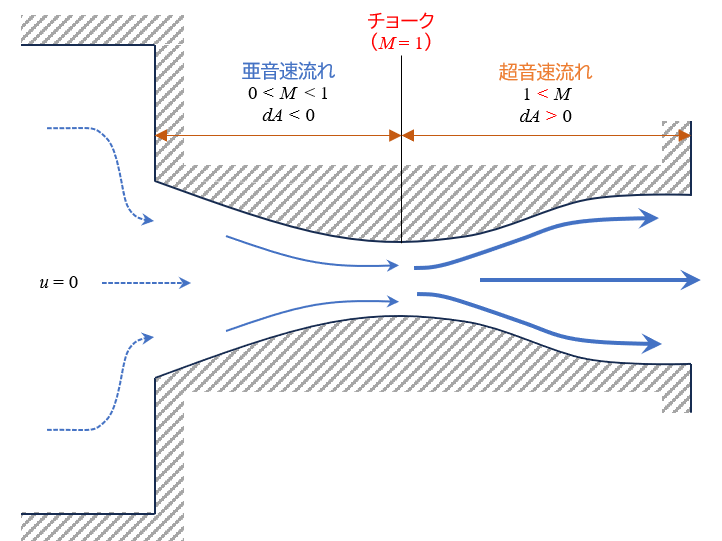
以上3点の特徴を絵にしたものが下の図です。
タンクなどの流速0の状態から管の断面積を絞っていくと、流体は加速していきます。
そして、M = 1のチョーク状態に到達し、それ以降は管を拡げていくことでさらに流体を加速する1ことができます。このようなノズルをラバールノズルといいます。
世の中のノズルの大半は、先端が絞られている先細ノズルです。この場合は、先細ノズルの先端2で流体は音速に達します。
臨界圧力比とチョーク
先ほどの図において、もしもタンクの圧力\(P_0\)と吹き出し先の圧力(背圧\(P_e\))の差が小さければ、流れは発生しません。
タンクの圧力を徐々に大きくしていって、あるところで流れがチョークしたとき、その時点のタンク圧と背圧の比を臨界圧力比といいます。
臨界圧力比は、下記の通り比熱比\(γ\)で決まります。理想気体では比熱比は1.4で計算します。
このときの臨界圧力比は0.528となります。
\(\dfrac{P_e}{P_0} = (\dfrac{2}{γ+1})^{\frac{γ}{γ-1}}\)
したがって、タンク内の圧力が背圧の約2倍となれば、最もノズルが細い位置で流れがチョークすることになります。
そして、これ以上タンクの圧力を上げても、背圧を下げても、チョークする場所は変わりませんし、チョーク地点における流速は音速となります。
質量流量の式
流れがいったんチョークしてしまえば、簡単に質量流量を求めることができるようになります。
なぜなら、質量流量の式における流速、断面積が固定されるからです。
実際は密度が圧力で変化するので、少しだけ式が複雑になります。
\( m = \dfrac{P_0A}{\sqrt{RT_0}}\sqrt{γ(\dfrac{2}{γ+1})^{\frac{γ+1}{γ-1}}} \)
ここで、
\(R \rm{:}ガス定数\rm{[J/(kg・K)]} \) ←一般ガス定数を気体分子量で除した値
\(T_0 \rm{:}ガス全温\rm{[K]} \)
このように、ノズルの口径、気体のタンク圧力、温度、種類がわかれば、流速を測らなくてもノズルを通過する質量流量を計算することができます。
オリフィスなどは、この原理を応用して流量を計測しています。
音速と背圧の影響
最後に、音速と背圧の影響についてまとめます。
一般に、流れの乱れ(専門用語では擾乱)は、圧力波の形で全方向に伝わります。
例えば、層流で流れる水の流れを速くしていくと、やがて下流のどこかで小さな乱れが発生します。
そしてその乱れは圧力の波となって上流側にも伝わり、瞬く間に流れが乱流に遷移していきます。
この圧力波は、流体の音速で伝わります。したがって、流れが音速以上となれば、圧力波は上流にさかのぼることができません。
つまり、下流の乱れの影響を受けないことになります。これは、実用上もメリットがあります。
例えば、エンジン内に燃料を吹き込む場合、エンジンの圧力は流れや燃焼圧の影響によって常に変化しています。
こういった条件下でも、燃料をチョーク状態で吹き込むことで、一定量の燃料を吹き込むことができます。
したがって、流れをチョークさせることで、安定して意図した通りの流量を流すことができるようになります。
まとめ
いかがでしたでしょうか。
今回の記事を通じて、圧縮性流れに関して苦手意識を持っている方の理解が進む一助になれば幸せです。
細かい内容や、式の導出方法について知りたい方は、以下の参考文献を参照してみてください。



コメント