【10分でわかる】流体力学でよく使われる無次元数の紹介

はじめに
無次元数とは
レイノルズ数
プラントル数
マッハ数
ヌセルト数
さいごに

はじめに

物理学の世界では自然現象を式に表して、それを解くことが一種の営みとなっています。
例えば有名なニュートンの万有引力では、リンゴが地面に落ちる様子からリンゴに加わる力を仮定して立式し、それを解いて得られる動きが月などの天体にも当てはまることを示しました。

このように、自然現象の背後にある法則や原理を見抜き、それを式に表すことができれば、あとはそれを解くことで、同様の現象を予測、説明することができるようになります。

流体力学もこの営みに沿って発展してきました。ですが、学問が発展するにつれて大きな問題が出てきました。それが、作った式が複雑すぎて手作業では解けない※という問題です。
※今のところ解けていないだけで、解けないと証明されたわけではありません。

下にその式（ナビエｰストークス方程式）を示しますが、式の長さだけでもその複雑さが感じ取れると思います。
\(\frac{D\boldsymbol{v}}{Dt} = -\frac{1}{\rho} \operatorname{grad} p+\frac{\mu}{\rho}\Delta\boldsymbol{v}+\frac{\chi +\frac{1}{3}\, \mu}{\rho} \operatorname{grad} \Theta
+\frac{\Theta}{\rho} \operatorname{grad}(\chi +\frac{1}{3}\, \mu) \)
\(+\frac{1}{\rho} \operatorname{grad}(\boldsymbol{v}\cdot \operatorname{grad} \mu)+\frac{1}{\rho} \operatorname{rot}(\boldsymbol{v}\times \operatorname{grad} \mu)-\frac{1}{\rho}\, \boldsymbol{v} \Delta\mu +\boldsymbol{g} \)

この問題に対しては、いくつかのアプローチがあります。コンピュータの発展に伴い、設計現場でも活躍してきている数値流体解析（CFD）もその1つです。

ですが、古典的には「対象の流れ場に関係ない項は削除して、式を簡単にして計算する」という手法がとられてきました。
このことから、対象の流れ場がどういった性質を持つかが、簡単に分析できることが重要だったのです。

無次元数とは

ここで役に立つのが無次元数です。
圧力や流速、流体の粘り気や熱の伝わりやすさといった流れ場の状態を無次元数に代入して計算すれば、その流れがどのような性質を持つかを教えてくれます。

無次元数にはたくさんの種類がありますが、この記事ではその中でも特に伝熱や流体分野で使用頻度が多い無次元数を取り上げます。

レイノルズ数

最も有名な無次元数です。流体がそのまま運動しようとする力（＝慣性力）と、流体を止めようとする力（＝粘性力）の比を示しています。アクセルとブレーキの比のイメージです。

レイノルズ数を計算して基準値（臨界レイノルズ数）と比べることで、流れが層流（規則正しく流れる）か、乱流（不規則に混ざり合いながら流れる）かを判別することができます。

\(Re = \dfrac{ρuL}{μ}　\)

\(ρ　\rm{：}密度\rm{[kg/m^2]} \)
\(u　\rm{：}流速\rm{[m/s]} \)
\(L　\rm{：}代表長さ\rm{[m]} \)
\(μ　\rm{：}粘性係数\rm{[kg/(m・s)]} \)

管の場合、このレイノルズ数が2300よりも大きい場合、流れは乱流となることが知られています。

プラントル数

境界層理論の第一人者であるドイツの物理学者ルートヴィヒ・プラントルの名前を冠した無次元数です。このプラントル数は速度境界層と温度境界層の比を示しています。

\(Pr = \dfrac{ν}{α} = \dfrac{μC_p}{k}　\)

\(ν　\rm{：}動粘性係数\rm{[m^2/s]} \)
\(α　\rm{：}温度拡散率\rm{[m^2/s]} \)
\(μ　\rm{：}粘性係数\rm{[kg/(m・s)]} \)
\(C_p　\rm{：}定圧比熱\rm{[J/(kg・K)]} \)
\(k　\rm{：}熱伝導率\rm{[J/(m・s・K)]} \)

境界層について少し補足します。
壁面近くでは摩擦によって流れが遅くなります。この遅くなった領域は壁に沿った層の形になり、主流と壁の境界に発達するため、速度境界層と呼ばれます。
また、流体の温度と壁の温度が異なる場合、同じように温度にも境界層が発達し、こちらは温度境界層と呼ばれます。

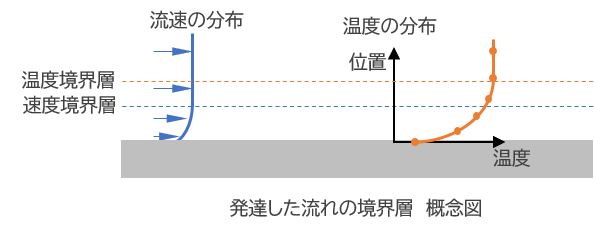
境界層の厚みは流体固有の値（物性値）によって決まるため、プラントル数も流体固有の値です。
（c.f. レイノルズ数は流れ場の状態で数値が変わる）

例えば粘り気が強い流体であれば、壁面との摩擦力も強くなって速度境界層は厚くなりますし、温度が伝わりやすい流体であれば、壁面からの温度がすぐに主流まで届くので温度境界層が薄くなります。

したがって、流れが同じ条件であれば、壁面近くに長くとどまって熱を早く伝える流体、すなわちプラントル数が1より大きい流体（速度境界層＞温度境界層）の方が、伝熱上有利となります。

マッハ数

マッハ数は流体の慣性力と弾性力（流れを圧縮するために必要な力）の比を表しています。
つまりマッハ数が大きいほど流れのアクセルが強く、流体自体が圧縮されやすいことを表しています。

\(Ma = \dfrac{u}{a} 　\)

\(u　\rm{：}流速\rm{[m/s]} \)
\(a　\rm{：}音速\rm{[m/s]} \)

マッハ数が0.3より小さい場合は、流れている流体をせき止めてもほとんど圧縮されないため、密度を一定として計算しても差し支えありません。（非圧縮性流体として扱える）
ですが0.3を超えると徐々に圧縮の影響が無視できなくなり、1を超えると超音速と呼ばれる状態となって、様々な挙動が劇的に変化します。

ヌセルト数

ヌセルト数は対流熱伝達と熱伝導の比を表しています。また、近似的には物体の代表長さと温度境界層の比を表しています。

\(Nu = \dfrac{hL}{k} ≅ \dfrac{L}{δ_T}　\)

\(h　\rm{：}熱伝達率\rm{[J/(m^2・s・K)]} \)
\(L　\rm{：}代表長さ\rm{[m]} \)
\(k　\rm{：}熱伝導率\rm{[J/(m・s・K)]} \)
\(δ_T　\rm{：}温度境界層厚み\rm{[m]} \)

ヌセルト数は他の無次元数とは使われ方が異なり、主に熱伝達率を求めるために使われます。
具体的には、レイノルズ数やプラントル数を計算したうえで実験式からヌセルト数を推定し、そのあとに上の定義式を逆算して熱伝達率を求める流れです。
詳細は「伝熱計算（熱交換器設計　二重円管）」の記事を参照してください。