熱交換器の伝熱計算

概要

一般的に、熱交換量は温度差と伝熱面積に比例することが知られています。
これはニュートンの冷却法則と呼ばれているもので、交換熱量は伝熱面積と温度差にそれぞれ
比例します。
\( \dot{Q} = UAΔT \)

\(\dot{Q}　　\rm{：}交換熱量[\rm{W}] \)
\(U 　 　\rm{：}総括熱伝達係数[\rm{W/(m^2・K)}] \)
\(A 　　\rm{：}伝熱面積[\rm{m}] \)
\(ΔT　\rm{：}温度差[\rm{K}]\)

よく知られたこの式ですが、実際に熱交換器の計算に使おうと思うと、
　①総括熱伝達係数はどう決めればよいのか？
　②温度差はどの数値を参照すればよいのか？
といった問題に直面します。

この記事を読むことで、熱交換器全般で使う伝熱計算が理解できるようになります。

計算前の準備

設計したい条件に合わせて、計算前に下記の情報を整理しておきましょう。
　■熱交換器内での、高温流体と低温流体の流れ方向
　■2流体それぞれの入口、出口温度、圧力、流量
　■伝熱管の材質
　■伝熱管の内外径
今回は、銅製二重円管を使って高温空気を低温水で冷却する向流型熱交換器（図1）について計算しましょう。

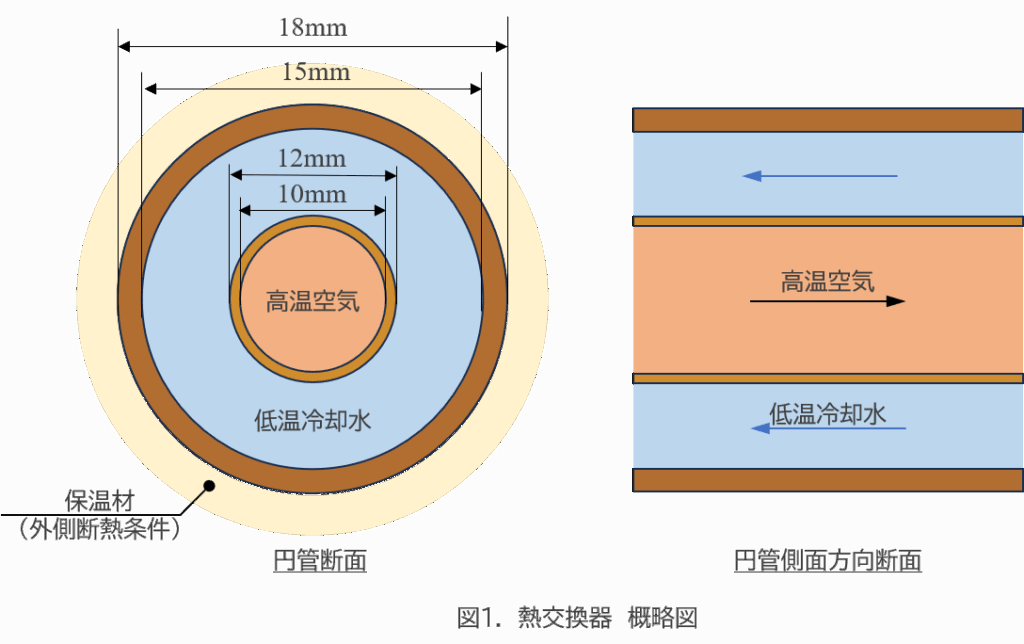
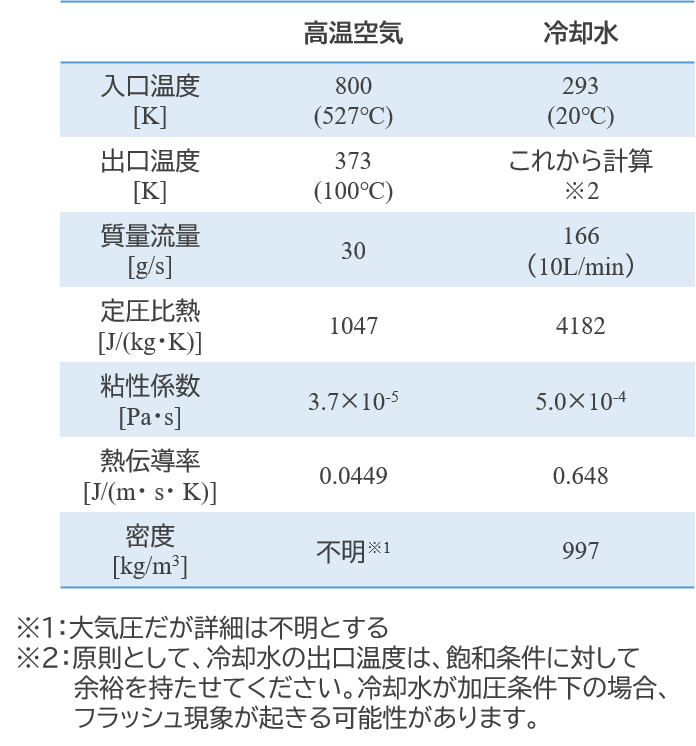
仕様と物性値は下記の通りとします。
より実践的な環境を模擬するため、空気側の密度は不明としました。

熱交換量の決定

まずは、今回設計する熱交換器で取り扱う熱量を計算します。
エネルギー保存則から、高温空気が失う熱量と、低温流体が得る熱量は等しくなります。
ただし、これは熱交換器外面から外部に逃げる熱が無視できること、空気や水の漏れがないことが前提となります。
今回は熱交換器の外側に十分な厚さの保温材を巻く（外側断熱条件）ことを仮定しています。
\( \dot{Q} = m_HC_H(T_{H\_in}－T_{H\_out})=m_LC_L(T_{L\_out}－T_{L\_in})\)

\(\dot{Q}　　\rm{：}単位時間あたりの交換熱量[\rm{W}] \)
\(m_○ 　 　\rm{：}質量流量[\rm{kg/s}] \)
\(C_○ 　 　\rm{：}定圧比熱[\rm{J/(kg・K)}] \)
\(T_{○\_in} 　 　\rm{：}入口温度[\rm{K}] \)
\(T_{○\_out} 　 　\rm{：}出口温度[\rm{K}] \)

添字
\(H　　\rm{：}高温流体\)
\(L　　\rm{：}低温流体\)

この式を用いると、必要な冷却量は
\( \dot{Q} = 30/1000 ×1047×(800－373)=13412.07=13.4\rm{kW} \)
であり、冷却水の出口温度は
\(T_{L\_out}=13412.07/(166/1000×4182)+293=312.3…=312\rm{K} \)
と計算できます。

対数平均温度差の計算

次に対数平均温度差（LMTD）を計算します。詳細はリンク先を参照して下さい。
今回は向流型なので、下記の通り計算できます。

\( ΔT_{LM} =\dfrac{[(T_{H\_in} – T_{L\_out}) – [(T_{H\_out} – T_{L\_in}) ] }{ln(T_{H\_in} – T_{L\_out}) / [(T_{H\_out} – T_{L\_in}) } \)
\( =[(800－312) － (373－293)] / ln[(800－312) / (373－293)]
=225.6… = 226\rm{K} \)

等価直径（水力直径、相当直径）と流路断面積の計算

今回は二重円管を採用しているので、冷却水が流れる流路断面はドーナツ状の円環となります。
この後の無次元数計算の際に、この円環断面と流れ場的に等価とみなせる円の直径を求める必要があります。
なお、等価直径についてはリンク先にもう少し詳しくまとめていますので、興味のある方は参照してみてください。
二重円管の場合、外径と内径の差が等価直径となります。
＜高温空気側＞
\(D_{eH} =10\rm{mm}=0.01\rm{m} \)
\(A_{H} =7.85×10^{-5}\rm{m^2}\)

＜冷却水側＞
\(D_{eH} =D_o－D_i =15－12\rm{mm} = 0.003\rm{m} \)
\(A_{L} =6.36×10^{-5}\rm{m^2} \)

レイノルズ数とプラントル数の計算

流れの特徴を分析するために、無次元数であるレイノルズ数とプラントル数を計算します。
それぞれの無次元数についての解説は、リンク先を参照して下さい。
今回は、高温空気側の密度が不明なので、質量流量と等価直径を使ってレイノルズ数を計算してみました。臨界レイノルズ数は、管内流れで一般に用いられる2300としています。
計算すると、いずれも乱流であることがわかります。

\(Re_H = \dfrac{ρud}{μ} = \dfrac{4m_H}{πμ_HD_{eH}}=\dfrac{4×30 /1000}{π×3.7×10^{-5}×0.01}=103236…>2300\)
\(Re_L = \dfrac{ρud}{μ} = \dfrac{4m_L}{πμ_LD_{eL}}=\dfrac{4×166 /1000}{π×5.0×10^{-4}×0.003}=15656…>2300\)

\(ρ　\rm{：}密度\rm{[kg/m^2]} \)
\(u　\rm{：}流速\rm{[m/s]} \)
\(d　\rm{：}円管直径または等価直径\rm{[m]} \)
\(μ　\rm{：}粘性係数\rm{[kg/(m・s)]} \)

このとき、等価直径を用いて流路断面積を計算してしまわないように注意してください。
等価直径ベースの流路断面積と、実際の流路断面積は必ずしも一致するわけではないためです。
等価直径は流れ場のスケールをあらわすために計算するものであり、幾何学的な等積変形をしているわけではありません。
対象の異形管と、同じ流れ場の特性を示す円管の直径を求めるための計算です。

プラントル数は下記のように計算できます。一般に空気は1以下、水は1以上となるので、定性的にも計算が合っていそうであることがわかります。

\(Pr_H = \dfrac{μC_p}{k}= \dfrac{μ_HC_{pH}}{k_H}=\dfrac{3.7×10^{-5}×1047}{0.0449}=0.8627…=0.863\)
\(Pr_L = \dfrac{μC_p}{k}= \dfrac{μ_LC_{pL}}{k_L}=\dfrac{5.0×10^{-4}×4182}{0.648}=3.226…=3.23\)

\(μ　\rm{：}粘性係数\rm{[kg/(m・s)]} \)
\(C_p　\rm{：}定圧比熱\rm{[J/(kg・K)]} \)
\(k　\rm{：}熱伝導率\rm{[J/(m・s・K)]} \)

ヌセルト数の計算

先ほど求めたレイノルズ数とプラントル数を使って、ヌセルト数を計算します。
ヌセルト数の式には熱伝達率が含まれているので、何らかの手法でヌセルト数を求めれば、そこから熱伝達率を逆算できるからです。

乱流熱伝達では、摩擦係数とヌセルト数の間にあるアナロジー（類似性）を使うと、下記のような関係（コルバーンのアナロジー）を導くことができます。
\(Nu = 0.5×C_f×Re×Pr^{1/3}\)

\(C_f　\rm{：}摩擦係数\rm{[－]} \)

この式の係数を実験データとフィッティングした相関式として、Dittus-Boelterの式がよく知られています。
この式は、レイノルズ数が\(10^3～10^7\)の範囲であれば、実験値とよく一致します。
\(Nu = 0.023×Re^{0.8}×Pr^n\)
ここで
　流体を加熱する場合：\(n=0.4\)
　流体を冷却する場合：\(n=0.3\)

先ほど計算したレイノルズ数は上記範囲内なので、上の式を用いてヌセルト数を計算すると、
\(Nu_H = 0.023×Re_H^{0.8}×Pr_H^{0.3} = 225.71… = 226\)
\(Nu_L = 0.023×Re_L^{0.8}×Pr_L^{0.4} = 83.365… = 83.4\)

という数値が得られます。

熱伝達率の計算

前項で求めたヌセルト数から、熱伝達率を計算します。
\(h_H = Nu_H×k_H/D_{eH} = 1013.46…=1013.5\)
\(h_L = Nu_L×k_L/D_{eL} = 18006.97…=18007\)

\(h_H　\rm{：}高温空気と配管表面間の熱伝達率\rm{[J/(m^2・s・K)]} \)
\(h_L　\rm{：}冷却水と配管表面間の熱伝達率\rm{[J/(m^2・s・K)]} \)

総括熱伝達係数の計算

最後に、熱交換器の熱の伝わりやすさを総括熱伝達係数（U値）を求めます。
前項で熱伝達率を求めましたが、これは実際の伝熱現象のうちの一部分の係数にすぎません。
図2に実際の伝熱の模式図を示します。

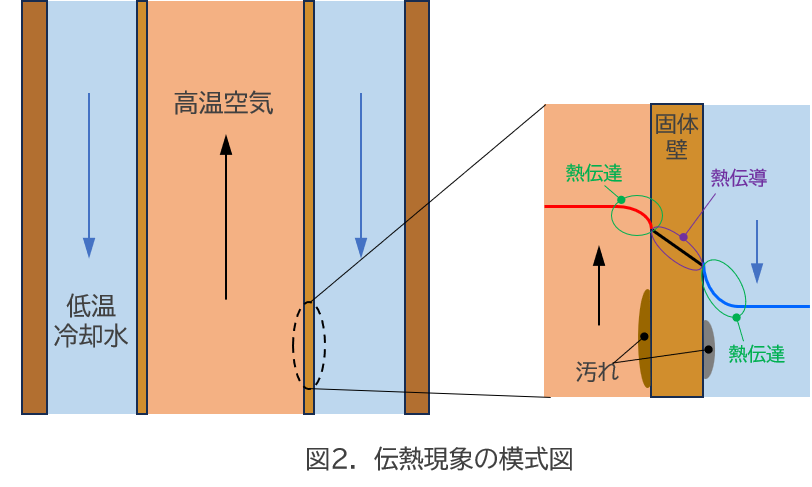
熱伝達率は、固体壁（配管壁）と流体の境における熱の伝わりやすさを表す係数のことです。
全体の伝熱を考えるうえでは、固体中の熱の伝わりやすさを表す熱伝導率や、汚れによる熱の伝わりにくさを表す汚れ係数も加味する必要があります。

これらを一つずつ段階的に計算する方法もあるのですが、計算が煩雑なので、1つの係数（総括熱伝達係数（U値） ）として計算してしまうことが多いです。
一般に、U値は下記のように計算することができます。

\(1/U = 1/h_H + δ/k_t + 1/h_L + R_H + R_L\)

\(δ　\rm{：}配管の肉厚\rm{[m]} \)
\(k_t　\rm{：}配管の熱伝導率\rm{[J/(m・ s・ K)]} \)
\(R_H　\rm{：}高温空気側の汚れ係数\rm{[m^2・K/W]} \)
\(R_L　\rm{：}冷却水側の汚れ係数\rm{[m^2・K/W]} \)

今回は銅管を使っているので、熱伝導率は370 J/(m・ s・ K)とします。
汚れ係数は、各種伝熱工学書籍に参考値が載っていますが、おおよそ0.0001～0.001程度です。
今回は空気側の汚れ係数は無視して、冷却水側の汚れ係数を0.0002としましょう。

\(1/U = 1/1013.5 + 0.002/370 + 1/18007 + 0 + 0.0002 ≒1.25×10^{-3} \)

したがって、\( U = 800 \rm{[J/(m^2・s・K)]}\)となります。

伝熱面積の計算

これまでに求めてきた値を使って、必要な伝熱面積を求めてみましょう。
記事の最初に記載したニュートンの冷却法則を変形して計算すると、

\(A = \dfrac{\dot{Q}}{UΔT_{LM}} = \dfrac{13.4×10^3}{(800×226)} = 0.074\rm{[m^2] }\)

となります。
したがって、外径12mmの管であれば約2～2.5mあれば仕様を満たすと推定されます。

実際の設計では、この結果をもとに
①機器のケーシングに収まるように管の本数や配置を調整
②配管の圧力損失を計算して必要なポンプの動力を計算
③装置の全体のイニシャルコストやランニングコストの計算
といった次のステップの検討を行います。

まとめ

いかがでしたでしょうか。
伝熱計算は流体力学や熱力学の知識を組み合わせる必要があるため、つまづきやすいポイントが多く、苦手意識を持っていた方も多いのではないでしょうか（筆者もその1人です）。

今回の記事を通じて、伝熱計算の理解が進む一助になれば幸せです。

より細かい内容や、式の導出方法、各種係数の数値について知りたい方は、以下の参考文献を参照してみてください。