流れ場のスケール
私たちがよく目にする世界では、流体の特性や状態量が流れ場を大きく左右します。
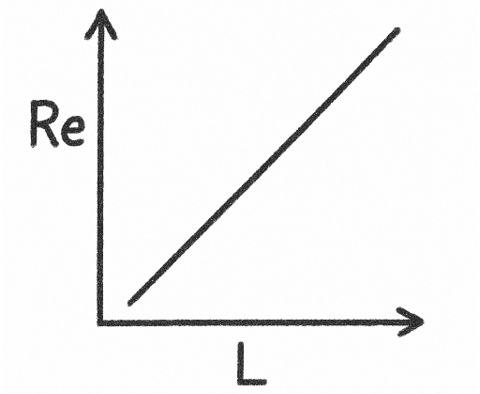
ですが、流体力学では「代表長さ」と呼ばれる場のスケールも流れ場の状態に影響を及ぼすことが知られています。最も有名な無次元数であるレイノルズ数で考えてみましょう。
\(Re = \dfrac{ρuL}{μ} \)
\(ρ \rm{:}密度\rm{[kg/m^2]} \)
\(u \rm{:}流速\rm{[m/s]} \)
\(L \rm{:}代表長さ\rm{[m]} \)
\(μ \rm{:}粘性係数\rm{[kg/(m・s)]} \)
例えば常温の空気の場合、密度が約\(1.3\rm{kg/m^2}\)、粘性係数が約\(1.8×10^{-5}\rm{kg/(m・s)}\)です。流速を\(1\rm{m/s}\)のそよ風とすると、私たちのスケール(L=1mオーダー)では、レイノルズ数は約70000で、さらさらとした慣性力支配の流れ場です。
ですが、これが昆虫などのサイズ(L=1mmオーダー)であればレイノルズ数は約70となり、どちらかというとドロドロとした粘性力支配の流れ場となってしまうのです。
(→クマバチが飛べる理由)
このように、流れ場の状態を考えるうえでは代表長さの選定が重要となります。
管路の代表長さと等価直径
どこのスケールを代表長さとするかは、対象の流れ場や検討したい現象によって異なりますが、
実用上もっとも扱われるであろう管内流れでは、管路の内側直径であらわすことが多いです。
扱う管がシンプルな円形断面であれば計算も簡単ですが、例えば河川のような矩形断面や、熱交換器でよく用いられる二重円管の場合はどうすればよいのでしょうか。
このようなときに役立つのが、等価直径(水力直径、相当直径)です。
流路の断面が単純な円ではない場合でも、直径の代わりに等価直径を使うことで、直径と同じように扱うことができます。
等価直径は下記の式で定義されます。ここで、濡れ縁長さとは流路内の周長のことです。
\(D_e = \dfrac{4A}{l} \)
\(A \rm{:}流路断面積\rm{[m^2]} \)
\(l \rm{:}濡れ縁長さ\rm{[m]} \)
この式で円形断面の等価直径を計算すると、実直径と一致します。
ですが、矩形や二重円管などで計算した等価直径を用いた流路断面積と、実際の流路断面積が一致するわけではないことに注意してください。
等価直径は流れ場のスケールをあらわすために計算するものであり、幾何学的な等積変形をしているわけではありません。
対象の異形管と、同じ流れ場の特性を示す円管の直径を求めるための計算です。
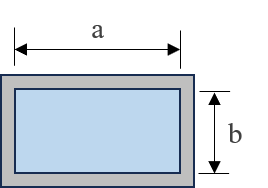
矩形断面の等価直径
高さ\(a\)、幅\(b\)の矩形断面における等価直径は、下記のように計算できます。
\(D_e = \dfrac{4ab}{2(a+b)}= \dfrac{2ab}{a+b}\)
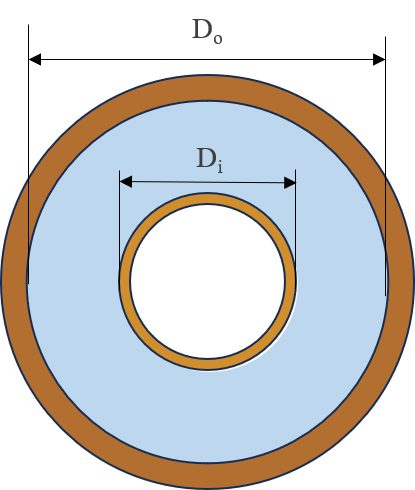
二重円管の等価直径
外管の直径を\(D_o\)、内観の直径を\(D_i\)とすると、流路断面積と濡れ縁長さはそれぞれ下記のようにあらわせます。
\(A = \dfrac{π(D_o^2-D_i^2)}{4} \)
\(L = π×(D_o+D_i) \)
よって、等価直径は
\(D_e =\dfrac{4×π(D_o^2-D_i^2)}{4}×\dfrac{1}{π×(D_o+D_i)}
=\dfrac{D_o^2-D_i^2}{D_o+D_i}
=\dfrac{(D_o+D_i)(D_o-D_i))}{D_o+D_i}
=D_o-D_i \)
したがって、二重円管の場合は外径と内径の差が等価直径となります。
さいごに
いかがでしたでしょうか。今回紹介した等価直径や流れ場のスケールについて、より知識を深めたい、という方には下記の教科書をオススメします。
本自体に厚みがありますが、実例も豊富で記載もわかりやすいので、興味のある方はぜひお手に取って調べてみてください。
また、等価直径を使った実際の熱交換器の計算については、こちらのページでまとめています。

コメント