熱交換器の伝熱計算でよく耳にする対数平均温度差について解説します。
ニュートンの冷却法則と交換熱量
伝熱学や熱力学を学んだ人であれば、交換熱量は下記の式で表せることはご存じかと思います。
これはニュートンの冷却法則と呼ばれているもので、交換熱量は伝熱面積と温度差にそれぞれ
比例します。
\( \dot{Q} = hAΔT \)
\(\dot{Q} \rm{:}交換熱量[\rm{W}] \)
\(h \rm{:}熱伝達率[\rm{W/(m^2・K)}] \)
\(A \rm{:}伝熱面積[\rm{m}] \)
\(ΔT \rm{:}温度差[\rm{K}]\)
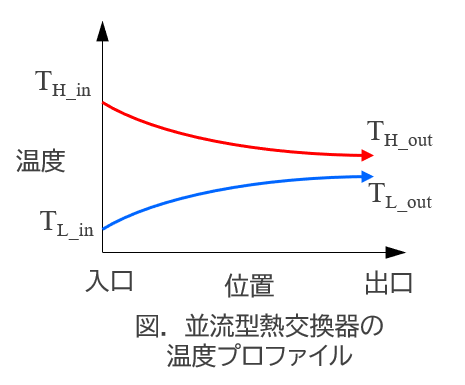
ですが、熱交換器の場合は図のように配管の位置によって流体同士の温度差が異なるため、
このままでは、各所の温度差から局所交換熱量を逐次計算して足し合わせる必要があります。
熱交換器の伝熱計算の多くの場合では、知りたいのはあくまで全体の交換熱量だけであり、局所的な情報はわからなくても構いません。
このようなシチュエーションで役立つのが対数平均温度差(LMTD)です。
対数平均温度差の計算式
対数平均温度差は、下記の式で計算可能です。
計算の際は、分母の中が引き算ではなく割り算であることに注意してください。
高温流体と低温流体が同一方向に流れる場合(並流)は、
\( ΔT_{LM} =\dfrac{[(T_{H\_in} – T_{L\_in}) – [(T_{H\_out} – T_{L\_out}) ] }{ln(T_{H\_in} – T_{L\_in}) / [(T_{H\_out} – T_{L\_out}) } \)
高温流体と低温流体が逆方向に流れる場合(向流)は、
\( ΔT_{LM} =\dfrac{[(T_{H\_in} – T_{L\_out}) – [(T_{H\_out} – T_{L\_in}) ] }{ln(T_{H\_in} – T_{L\_out}) / [(T_{H\_out} – T_{L\_in}) } \)
この対数平均温度差を、冒頭に説明したニュートンの冷却法則の温度差の部分に用いることで、
熱交換器の場合でも交換熱量を簡単に算出することができるため、非常に便利です。
なお、上の式の導出は下記の教科書にて参照できますので、興味のある方は調べてみてください。
(熱交換の微分方程式から温度プロファイルを求め、そのプロファイルを区間全体で積分することで得られます。)



コメント